CS188人工智能课程翻译

发表于 | 更新于
CS188人工智能课程翻译

前文内容

英文实在看不下去了

[TOC]

强化学习

RL I notes

在前面的笔记中，我们讨论了马尔可夫决策过程(Markov decision processes, MDP)，即通过值迭代(value iteration)和决策迭代(policy iteration)的方式去计算状态的最优价值(optimal value of states)并得到最优策略(optimal policy)。解决马尔可夫决策过程是 离线规划(offline planning) 的一个例子，此时 agent 知道每一处的转换函数(transition function)和奖励函数(reward function)，所有用来预处理最有价值的信息都不需要任何操作(action)来获取。在这节中，我们将讨论 在线规划(online planning) ，此时 agent 对任何一处的转换函数和奖励函数都一无所知。在在线规划中，agent 必须尝试 探索(exploration) ，在探索中它进行操作(actions)并在后继状态(successor states)得到反馈(feedbacks)并得到相应的奖励(rewards)。agent用反馈的信息去估计(estimate)最优策略，这个过程被称作 强化学习(reinforcement learning) ，再用估计过的最优策略去探索或者说使奖励最大化(reward maximization)。

先从基本的术语开始。在在线规划的每一步，agent 从状态 $ s $ 出发，然后通过操作 $ a $ 最后到达后继状态 $ s’ $ ，获得奖励 $ r $ 。每一个多元组 $ (s, a, s’, r) $ 被称作 样本(sample) 。 agent 持续地进行操作并在后继状态收集样本直到到达结束状态(terminal state)。像这样的一组样本(a collection of sample)称作一个周期(episode)。agents会进行多个周期以得到足够的数据进行学习。

有两种强化学习的类型——基于模型的学习(model-based learning)和不基于模型的学习(model-free learning)。基于模型的学习尝试用样本去估计转换和奖励函数，再用这些估计进行MDP（值迭代、策略迭代）。不基于模型的学习尝试去直接估计状态的 Q 值(Q-values of states)，而不用空间去构造MDP中转换函数和奖励函数的模型。

基于模型的学习

用某个策略 $ \pi_{explore} $ 探索。

agent 生成转换函数的近似值 $ \hat{T}(s, a, s’) $ ，通过记录从 Q 状态 $ (s, a) $ 转换到状态 $ s’ $ 的次数，并规范化（即古典概率， $ \hat{T}(s, a, s’) = \frac{count((s, a) \rightarrow s’)}{count((s, a))} $ ）。根据大数定律，收集的样本越多， $ \hat{T} $ 越接近真实值。

agent 生成奖励函数 $ \hat{R} $ ，通过不断探索未知的多元组 $ (s, a, s’) $ 。

当我们觉得合适的时候，我们结束 agent 的训练(training)，通过值迭代或者策略迭代在当前的模型（包含 $ \hat{T}, \hat{R} $ ）生成开发策略 $ \pi_{exploit} $ ，目标是使奖励最大化。我们将要讨论如何有效地在探索(exloration)和开发(exploitation)之间分配时间的方法。

基于模型的学习简单易懂且高效，但是维护所有收集的多元组 $ (s, a, s’) $ 的成本昂贵（空间、时间），所以在下一节——不基于模型的学习，我们将开发一种方法，免于多元组 $ (s, a, s’) $ 的维护，避免基于模型学习的内存开销。

不基于模型的学习

有很多不基于模型的学习算法，我们将讲以下三种：直接估值(direct evaluation)，时间差异学习(temporal difference learning)和 Q-learning 。直接估值和时间差异学习属于 被动强化学习(passive reinforcement learning) 的一类算法。在被动强化学习中，agent 遵循已知的策略操作并在过程中得到状态的值，这正是在 $ T $ 和 $ R $ 已知时 MDP 的策略评估所做的。 Q-learning 属于另一类不基于模型的学习—— 主动强化学习(active reinforcement learning)，即agent在学习过程中可以通过反馈多次更新策略并最后经历足够多的探索后决定最优策略。

直接估值

先确定一个策略 $ \pi $ ，然后让 agent 遵循策略 $ \pi $ 进行多个周期。在 agent 收集样本的同时也维护每个状态下得到的价值和(counts of the total utility)以及 agent 访问到每个状态的次数(the number of times it visited the state)。任何时候，我们可以计算任意状态 $ s $ 的价值（即期望收益）：状态 $ s $ 的价值和除以状态 $ s $ 的访问次数。

例子：

策略 $ \pi $ 如下，衰减系数 $ \gamma = 1 $ ，每条边奖励函数为 $ -1 $ 。

fig1.png

状态 C 有概率走向状态 A 和状态 D，在探索次数较少时，从状态 B 出发和从状态 E 出发可能导致计算出的期望收益不同。在探索次数增多后会收敛成同一个值，但是这将会花费大量的时间。这个问题可以通过另一个被动强化学习——时间差异学习(temporal difference learning)来减轻。

时间差异学习

时间差异学习(temporal difference learning， TD learning)用了从每一次经历中学习的想法，而不是像直接估值那样先对状态价值和以及访问次数统计再做学习。在策略评估中，我们用固定的策略生成的方程组和 Bellman 方程组决定状态的值（或者迭代更新，像值迭代一样）。

TD learning 尝试去解决如何在没有权重的情况下计算加权平均值的问题，用 指数滑动平均(exponential moving average) 的方式。

步骤：

  1. 初始化：
  1. 对于每一步，agent 进行操作 $ \pi(s) $ ，从状态 $ s $ 转移到状态 $ s’ $ ，获得奖励 $ R(s, \pi(s), s’) $ 。我们可以得到样本值(sample value)：

$ \space \space \space \space \space \space $ 这是对 $ V^{\pi}(s) $ 的新的估计。

  1. 将样本值用指数滑动平均的方式纳入对 $ V^{\pi}(s) $ 的估计，对 $ V^{\pi}(s) $ 进行更新 ：

$ \space \space \space \space \space \space $ 其中 $ \alpha (0 \leq \alpha \leq 1) $ 被称为 学习速率(learning rate) 。

由这个更新规则可知，越旧的样本的权重指数级减小，这正是我们更新 $ V^{\pi}(s) $ 所需要的（因为越旧的样本往往意味着较劣的策略，也意味着错误）！这就是 TD learning 的美妙之处——用一个简单直接的更新规则，我们能够：

  • 在每一步学习，因此没得到状态的值的信息可以直接使用。
  • 给较旧的、不太准确的样本给予指数级减小的权重。
  • 相比于直接估值，可以在更少的周期内更快地向正确的状态的值收敛。

Q-learning

无论是直接估值还是 TD learning ，它们都会在所遵循的策略下得到真实的状态的值。但是，它们都有一个固有的问题——我们想要找一个最优的策略，这需要知道每个状态的 Q 值。为了计算 Q 值，我们需要转换函数和奖励函数并用 Bellman 方程表示。

因此，为了高效地更新 agent 的策略，TD learning 和直接估值通常与一些基于模型的学习一起使用，以获得 $ T $ 和 $ R $ 的估计。这种情况可以通过 Q-learning 的思想避免，即绕过对转换函数、奖励函数的需要，直接对 Q 值进行学习。因此，Q-learning 是完全不基于模型的。Q-learning 用了 Q 值迭代进行更新：

有了这个新的更新规则，和 TD learning 一样，用指数滑动平均：

只要我们花足够多的时间去探索，并且用恰当的速率去减小 $ \alpha $ ，Q-learning 会对每个 Q 状态得到最优的 Q 值。这使得 Q-learning 具有革命性的意义——当 TD learning 和直接估值在某个策略下得到状态的值再用其他技巧决定最优策略时，Q-learning 可以直接得到最优策略，即使做出的次优或者随机的操作。这就是所谓的 离线策略学习(off-policy learning) （相较于直接估值和 TD learning 作为 在线策略学习(on-policy learning) 的例子）。

Approximate Q-learning

Q-learning 还有进步的空间。Q-learning 将所有的状态以表格的形式存储，当状态数很多时，Q-learning 的效率并不高。这意味着我们不能访问所有状态并且不能存储所有的 Q 值，因为空间不够。

假如一个局势下 Q-learning 判断出是不利的，那么对于类似的情况 Q-learning 无法判断也是不利的。Approximate Q-learning 尝试去学习一些一般的情况并外推到许多类似的情况来解释这一点。生成学习经验的关键是对状态的 基于特征的表示(feature-based representation) ，即用一个 特征向量(feature vector) 来表示状态。例如，吃豆人的特征向量可以编码为：

  • 距离最近的幽灵的距离
  • 距离最近的食物的距离
  • 幽灵的个数
  • 吃豆人是否被困(True/False)

使用特征向量，我们可以将状态的值和 Q 值视为线性函数：

其中 $ \vec{f}(s) $ 表示状态的特征向量，$ \vec{f}(s, a) $ 表示 Q-状态 $ (s, a) $ 的特征向量，$ \vec{w} $ 表示权重向量。定义偏差(difference)为：

Approximate Q-learning 的更新规则和 Q-learning 完全一致（实际上是最小二乘，不知道为什么笔记里写的是和 Q-learning 更新方式一致的）：

放弃对每个状态的 Q 值存储，使用 Approximate Q-learning 我们只需要存储一个权重向量就可以计算需要的 Q 值。因此，这不仅给了我们一个更泛用的 Q-learning 版本，并且显著提升了存储效率。

用偏差来重写 Q-learning 的更新规则：

这个更新规则和 $ w_{k} \leftarrow w_{k} + \alpha \cdot difference \cdot f_{k}(s, a) $ 略有不同但同样具有价值：它计算估计值和当前值的偏差，然后往估计值方向趋近，幅度和偏差值成正比。

（note 里没写，PPT 里讲地不清楚，视频里一笔带过，以下内容疑似 PPT 内容的机翻）

问题：通常，运行良好的基于特征的策略（能赢，最大化得分）不是去选 V 值或者 Q 值最好的策略。

解决方案：学习奖励最大化的策略，而不是预测的值。

策略搜索：从一个不错的策略开始（例如：Q-learning 生成的策略），然后（在特征权重(feature weights)上）用爬山微调。

最简单的策略搜索：

  • 从线性的初始状态值或者 Q 值开始。
  • 稍稍增加或者减小每个特征的权重，然后观察策略是否更优。

问题：

  • 我们怎样认为这个策略更好？
  • 这需要运行很多次样例的周期！
  • 当特征很多时，这种方法就显得不实用。

更好的方法利用前瞻性结构(lookahead structure)，聪明地取样，改变多个参数等等。

RL II notes

RL II slides

探索和开发(exploration and exploitation)

如何去探索？

最简单的方式：随机操作( $ \varepsilon $ - greedy)

  • 每一步，进行两种选择。
  • 一个较小的概率 $ \varepsilon $ ，随机操作。
  • 一个较大的概率 $ 1 - \varepsilon $ ，按当前策略操作。

随机操作的问题：

  • 最终会探索整个空间，但一旦完成了学习，就会到处乱走。
  • 一个解决方法： $ \varepsilon $ 随时间减小。
  • 另一个解决办法：用探索函数(exploration functions)。

探索函数(exploration functions)

对于随机操作，可以探索一定次数后结束。

更好的想法是，去探索访问次数少的点，最后停止探索(explore areas whose badness is not (yet) established, eventually stop exlporing)。

用估计的值 $ u $ 和访问次数 $ n $ 来定义探索函数，返回一个乐观的估计，例如 $ f(u, n) = u + k / n $ 。

对 Q 值更新规则进行修改：

反悔(regret)

即使你能找到最优策略，在过程中你依旧可能会犯错误。

反悔值是你衡量错误成本的指标：最优（期望）的奖励和你（期望）的奖励（包括早期的次优选）的差。

最大限度地减少反悔不仅仅是为了得到最优策略，它还需要最优化学习以达到最优策略。

例如：随机探索和用探索函数探索都能得到最优策略，但是随机探索有更高的反悔值。

概率

Probability slides

Probability notes

条件独立：事件A，B关于事件C条件独立（只要C事件发生，A、B相互独立），当且仅当：

记作：

推导：

贝叶斯网络

BN: Representation slides

BN: Representation notes

贝叶斯网络表达(Bayesian Network Representation)

虽然枚举可以计算我们所有想要知道的概率，在计算机中用内存存储所有的联合分布(joint distribution)对于实际问题是不切实际的——假如有 n 个变量，每个变量有 d 个取值，那联合分布表会有 d^n^ 个条目，呈指数级。

贝叶斯网络通过条件概率(conditional probility)避免了这个问题。概率被存储在一些小的条件概率表并用有向无环图(directed acyclic graph, DAG)描述变量之间的关系。本地的概率表和DAG一起将信息存储，并足以计算任何条件概率分布。

我们定义贝叶斯网络包含：

  • 一个DAG，一个节点表示一个变量 $ X $ 。
  • 对于每个节点有一个条件概率分布 $ P(X | A_1 \dots A_n) $ ，其中 $ A_i $ 表示 $ X $ 的第 $ i $ 个父亲，用条件概率表(conditional probability table, CPT)存储。每个CPT含有 $ n + 2 $ 列：$ n $ 个父亲，一个 $ X $ ，还有一个条件概率。

贝叶斯网络的结构对不同节点间条件独立关系进行编码。这些条件独立性使我们可以存储多个小表，而非一个大表。

很重要的一点是贝叶斯网络节点之间的边并非表示两者之间存在相关性，不是因果关系。

例如，假设有一个模型，包含5个二进制随机变量：

  • B：发生盗窃
  • A：警报响起
  • E：发生地震
  • J：John报警
  • M：Mary报警

它们的关系可以用下图表示。

fig2.png

在贝叶斯网络里，我们存储概率表 $ P(B), P(E), P(A | BE), P(J | A), P(M | A) $ 。

我们可以计算概率：

例如：

贝叶斯网络结构(Structure of Bayes Nets)

即 $ x_i $ 与 $ x_1, x_2, \dots x_{i - 1} / parents(x_i) $ 在 $ parents(x_i) $ 下条件独立。

例如：

fig2.png

一一对应可得条件独立关系。

每个节点与其马尔可夫覆盖(Markov blanket)之外的点条件独立。

一个变量的马尔可夫覆盖包含它的父亲、儿子和儿子的其他父亲（因为是DAG）。

D分离(D-Seperation)

Slides

D分离（D-Separation）又被称作有向分离，是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法，D-Separation更加直观且计算简单。对于一个DAG（有向无环图），D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。

查询：$ x_i \perp x_j \vert \{x_{k_1}, x_{k_2}, \dots x_{k_n}\} $

检查所有连接 $ x_i $ 和 $ x_j $ 的路径。如果一条或者多条路径是 激活 的，那么，条件独立性不成立。

否则，条件独立性成立： $ x_i \perp x_j \vert \{x_{k_1}, x_{k_2}, \dots x_{k_n}\} $ 。

如果路径中所有的三元组都是 激活 的，则该路径是 激活 的。

三元组的三种形式（又或者没有证据变量）：

  • 因果链条

A(0) -> B(1) -> C(0)

链上的中间变量可以阻隔影响传播。

  • 共同原因

    A(0) <- B(1) -> C(0)

  • 共同结果

    A(0) -> B(1) <- C(0)

如果路径中某三元组是非激活的，那么这条路径就是非激活的。

贝叶斯网络独立性问题的形式化定义

  • 问题：给定证据变量(evidence variables) $ \{Z\} $ ， $ X $ 是否条件独立于 $ Y $ ?

  • D-分离：在贝叶斯网络中寻找关联路径，并基于路径作独立性判断。

  1. 列出所有连接 $ X $ 和 $ Y $ 的路径。
  2. 没有激活路径 = 独立性，有激活路径 = 独立性不成立。
  • 路径的独立性判断：将路径拆解为多个三元组，检查三元组的独立性。

激活 / 非激活路径

如果每个三元组都是激活的，那这条路径就是激活的。

  • 因果链条：若 $ B $ 未被观察， $ A $ 和 $ C $ 不相互独立；否则相互独立。
  • 共同原因：若 $ B $ 未被观察， $ A $ 和 $ C $ 不相互独立；否则相互独立。
  • 共同结果：若 $ B $ 或者其子孙节点未被观察， $ A $ 和 $ C $ 相互独立；否则不相互独立。

出现不独立的情况，这个三元组就被激活。

如果任一三元组不激活，这条路径就不激活。

贝叶斯网络中的条件独立性

给定贝叶斯网络，运用 D-分离 方法，可以得到所有形式的条件独立性。

基于得到的条件独立列表，可以确定贝叶斯网络能够表达的所有概率分布。

贝叶斯网络的独立性隐含关系

给定贝叶斯网络，只有特定的联合分布能够被表达。

贝叶斯网络中的某些（条件）独立性，确立了能被表达的联合分布。

表达扩充：在贝叶斯网络中增加边，可以扩充能表达的分布范围。

极端情况：节点不存在独立性，能表达任意分布。

概率推断

Slides

询问

枚举

通常情况：

  • 证据变量： $ e_1, e_2, \dots , e_k $
  • 询问变量： $ Q $
  • 隐藏变量： $ H_1, \dots , H_r $

步骤：

  1. 选出包含证据变量的条件概率表的条目。
  2. 将 $ H $ 相加：
  1. 规范化

时间复杂度是指数级的，能够得到准确的答案。

消元法

联合分布 $ P(x y) $ 的和为 $ 1 $ 。

选定几个节点固定： $ P(x Y) $ 。这是联合分布的一部分，其和为 $ P(x) $ 。

大写字母（未确定变量）的个数即概率表的维数。

单个条件概率： $ P(Y | x) $ 。

  • 包含所有 $ P(y | x) $ 的固定 $ x $ 的条目。
  • 和为 $ 1 $ 。

条件概率组： $ P(Y | X) $ ：

  • 包含所有 $ P(y | x) $ 的所有条目。
  • 和为 $ X $ 的集合大小 $ |X| $ 。
步骤

一个一个消除隐藏变量。要消除隐藏变量 $ X $ ，我们要：

  1. 将包含 $ X $ 的因子(factor)乘起来。
  2. 加起来消除 $ X $ 。

一个因子定义为未被规范化的概率。在变量消除期间的所有时候，每个因子都将与其对应的概率成正比，但每个因子的基础分布不一定像概率分布那样总和 $ 1 $ 。伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
def elimination(X, e, bn): # returns a distribution of X
    # X : query variable.
    # e : observed values for variables E(evidence variables).
    # bn : a Bayesian network specifying joint distribution
    # P(x1, ..., xn).
    factors = []
    for var in ORDER(var, e):
        factors = [MAKE_FACTOR(var, e) | factors]
        if var is hidden variable:
            factors = SUM_OUT(var, factors)
    return NORMALIZE(POINTWISE_PRODUCT(factors))

（CS188 Notes 里写得和天书一样）

举个例子：

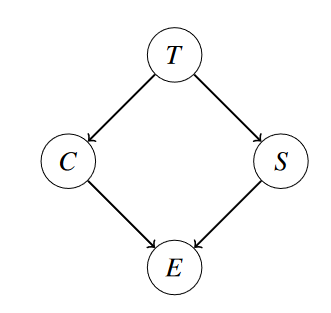
fig3.png

这个贝叶斯网络给定了 $ P(C), P(C | T), P(S | T), P(E | CS) $ 的联合分布。

假设我们要求 $ P(T | +e) $ 。假如用枚举的方法我们需要 16 行的概率分布函数 $ P(T, C, S, E) $ ，选择包含 $ +e $ 的行，对 $ C, S $ 求和最后规范化。

用消元法就先将 $ C $ 消掉，再把 $ S $ 消掉。

  1. 将包含 $ C $ 的因子乘起来， $ f_1(C, +e, T, S) = P(C | T) \cdot P(+e | C, S) $ ，也写作 $ P(C, +e | T, S) $ 。
  2. 在这个新的因子里将 $ C $ 求和，得到新的因子 $ f_2(+e, T, S) $ ，也写作 $ P(+e | T, S) $ 。
  3. 将包含 $ S $ 的因子乘起来， $ f_3(+e, T, S) = P(S | T) \cdot f_2(+e, T, S) $ ，也写作 $ P(+e, S | T) $ 。
  4. 将 $ S $ 求和，得到新的因子 $ f_4(+e, T) $ ，也写作 $ P(+e | T) $ 。
  5. 将剩下的因子乘起来，$ f_5(+e, T) = f_4(+e, T) \cdot P(T) $ 。

消元的顺序也会影响复杂度。如图：

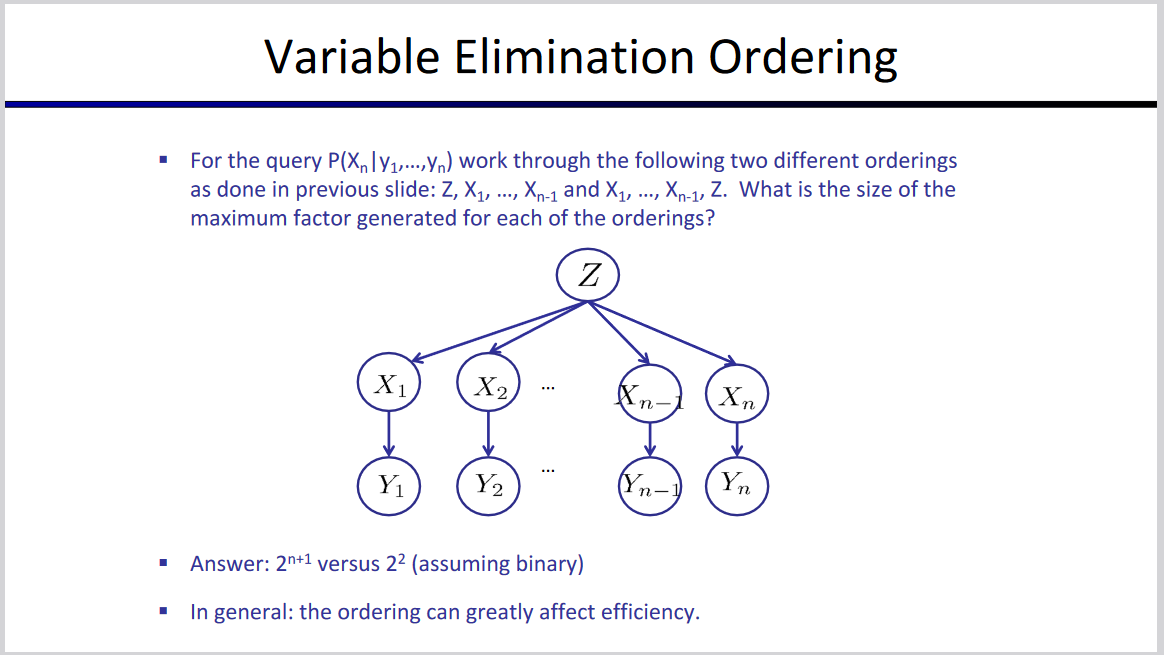
fig4.png

我们在进行变量消除的过程中，会进行多次乘法，这就可能会产生各种尺寸的因子，如果最大的因子中有 $ w $ 个变量，那么，单次消元的代码复杂度为 $ O(2^w) $ 。我们把 $ w $ 这个数字称为消除顺序 (Elimination Order) 的宽度 (Width)，这是衡量一个消除顺序的重要指标，我们希望能找到一个具备最小宽度的消除顺序，也就是希望最大因子的尺寸尽可能小。

概率推断是 NPC 问题

Slides 提到了一种用贝爷斯网络构造 3-sat 问题的方法。众所周知 3-sat 是无法在多项式时间复杂度内解决的问题，所以概率推断是 np-hard 的。

取样(sampling)

基本思想

  • 从分布 S 中取 N 个样本。
  • 计算后验概率。
  • 体现这个概率收敛于真实概率 P 。

先验采样(Prior Sampling)

1
2
3
For i = 1, 2, ..., n
    Sample x_i from P(X_i | Parents(X_i))
return (x_1, x_2, ..., x_n)
  • 这个过程生成样本，其中有 $ P(x_1, \dots, x_n) $ 的概率生成样本 $ (x_1, \dots, x_n) $ 。
  • 令一个事件的样本数量为 $ N_{PS}(x_1, \dots, x_n) $ 。

拒绝采样(Rejection Sampling)

1
2
3
4
5
6
Input: evidence instantiation
For i = 1, 2, ..., n
    Sample x_i from P(X_i | Parents(X_i))
    if x_i not consistent with evidence
        return: reject this sample
return (x_1, x_2, ..., x_n)

在 Prior Sampling 的基础上把不符合条件（不满足证据变量条件）的样本直接在采样的时候删去。

Likelihood Weighting

  • rejection sampling 的问题：当证据变量的概率很小时，会拒绝很多样本。
  • Idea：直接固定证据变量(要赋予一定的权重，大小为得到证据变量的条件概率)。
1
2
3
4
5
6
7
8
9
Input: evidence instantiation
w = 1.0
For i = 1, 2, ..., n
    if x_i is an evidence variable
        X_i = observation x_i for X_i
        set w = w * P(x_i | Parents(X_i))
    else
        sample x_i from P(x_i | Parents(X_i))
return (x_1, x_2, ..., x_n), w
  • Likelihood Weighting 的问题：Evidence influences the choice of downstream variables, but not upstream ones (C isn’t more
    likely to get a value matching the evidence) （没看懂，大概是拓扑序前面的节点会影响后面的节点，但是后面的节点不会对前面的节点有影响，但这怎么成了问题）（哦，大概是条件概率表不构成拓扑关系，这时候就不能用之前的方式）

吉布斯采样(Gibbs Sampling)

假设有一随机向量 $ (x_1,x_2,\dots,x_n) $ ，每一维是一随机变量。

显然想要从多元分布的联合概率分布中直接抽样是相当困难的。

先从任意一个初始状态 $ (x_1^{(0)}, \dots, x_n^{(0)}) $ 开始，每一维度单独采样，迭代多次。

1
2
3
4
5
6
7
for t = 1, 2, ..., T
    for i = 1, 2, ..., n
        if x_i is not an evident variable
            sample x_i^{(t)} from P(x_i | (x_1^{(t - 1)}, ..., x_n^{(t - 1)}) \ x_i^{(t - 1)})
        else
            x_i^{(t)} = x_i^{(t - 1)} (remain the evident value)
    cnt[(x_1^{(T)}, ..., x_n^{(T)})] += 1